数学之美学习笔记

文章发布时间:

最后更新时间:

《数学之美》读后感

本书在各个方面深入浅出地科普了数学在IT上的应用。虽然我认为其中的数学知识不算太多，因为作者原本的目的也是想让某些IT公司了解到在IT行业做事情的正确方法——重视简单而有效的方法而非凑合。所以我看完本书后数学美不美没看出来，反正计算机是挺美的。基本上是关于人工智能的。

本书因为原本是以博客为载体，所以所分成的34章之间没有太大的关联，适合碎片化阅读。其又将难点作为延展阅读分出来，对只想浅层了解的读者很好。

下面展开回顾一下其中的知识和我认为有用的点。

自然语言处理

语言与通信

作者讲到，语言的本质是为了人类之间的通信，所以所有自然语言处理的问题都可以等效为通信的解码问题。科学家由此发明了基于统计的算法，此方法遥遥领先于基于规则的算法。这种算法找到了语言的本质，把自然语言处理，机器翻译，语音识别等问题都概括成通信模型（编码和解码的过程），从而找到又简单又通用的方法。这也让我认识到计算机与人类的本质不同，所以凭直觉地让计算机模仿人类很多是低效的。（基于语法规则和理解文义的算法的失败）

统计语言模型

通过计算每句可能的句子的概率（）来生成最有可能的句子。它基于马尔可夫假设推出这样一个公式： 这称为二元模型。当然也有更高阶的模型，但有更大的时间和空间复杂度（ ）。统计语言模型只需要在巨大的语料库里统计 。

由于统计数据中小概率和零概率事件的可靠性低，所以需要做平滑过渡处理。对于未看见的事件，我们需要从总量（100%）中分配很小的比例给它们，根据”越是不可信的统计折扣越多“的方法（古德-图灵公式）。高阶模型则会用卡茨退避法。

训练之前还需要进行噪音过滤。

分词

与上述的模型相似。但需要注意的是，应用不同时汉语分词的颗粒度大小时常不同。比如机器翻译的颗粒度应该更大，而搜索引擎的颗粒度应该更小，需要根据所需进行改良。

隐马尔可夫模型

它的定义大致是这样（具体定义见维基）：令 ， 为离散时间随机过程， 是马尔可夫过程（就是一条马尔科夫链， 只与 有关， 只与 有关， 不可观测， 可观测（确定）。因此输出符号的序列（ ）能够透露出状态序列（ ）的一些信息。公式为 其在通信模型中的理解就是{O_n}是要解码的序列，{S_n}是解码后得到的序列，我们需要挑出P(s_1,s_2,...|o_1,o_2,...)最大的{S_n}来作为答案。

隐马尔可夫模型的参数可以通过鲍姆-韦尔奇算法得到。它只需要大量{O_n}，是一种无监督的训练方法。大致算法（我理解的）如下：它可以得到生成{O_n}的所有路径和概率，然后通过改变参数使得观测序列出现的概率最大化。具体算法详见维基百科

此模型非常通用，除自然语言处理之外还有很多问题可以用到这个算法。

信息论相关

信息熵

信息熵可以度量一个信息的作用，可以理解为在不知道一条信息的情况下提供多少bool信息（是or否）能完全知道它。其计算公式为 s为未知量的任意可能状态。

作者还提到了条件熵的概念，其公式为 还有互信息（度量两个随机事件的相关性）

搜索引擎

基本原理

  • 自动下载尽可能多的网页（爬虫）
  • 建立索引（基于数据库和布尔运算）
  • 对相关网页排序

PangRank算法

它的基本原理非常简单，就是“如果一个网页被很多网页所链接，那么它的排名就高”。

其排名的依据应该是每个指向它的网页的排名之和，公式大致为 指向的网页 用矩阵表示就是 其中 ， 为以网页为点，超链接为边的邻接矩阵。然后就可以使用迭代的方法。

因为网页数量巨大，还可以使用稀疏矩阵的方法简化计算量。

除此之外，还要进行平滑处理，改进公式如下

搜索关键词权重的度量 TF-IDF

在一个网页的关键词中，有的关键词比如‘的’，’应用‘因为非常常见，所以没有那么重要；而有一些关键词比如’TF-IDF‘就非常重要，所以发明了TF-IDF的概念。TF指单文本词频，就是一个词语在这篇文章中的重要性。IDF是逆文本频率指数，它的公式是 总网页数所出现的网页数 则一个搜索语句和一篇网页的相关性可以用以下公式来度量 搜索中的关键词 这其实与信息论的公式很相似。

网页权威性计算

与PageRank大致相同，但是用文章内容中的“提及”而不是超链接的指向，而且权威性要分主题。

问题：如何通过描述找到网站，如何区分权威网站和套壳网站？

有限状态机

用于地址识别时很有效，因为地址的文法简单，有明显的从属关系。还可以在自动机器人控制，编译器和解释器，网络协议等方面应用。

分类

特征向量

找到和文章主题相关的所有词语（总TF-IDF高）作为单词库。定义一篇文章的特征向量为它在单词库里的词语的TF-IDF值（注意是相对于这篇文章来说）所组成的向量。则两个向量的相关性可以用它们的夹角的余弦值表示。

那么分类的方法可以用自底向上不断合并，但比较复杂且耗时比较长，而下面一种办法能一步到位。

奇异值分解（SVD）

SVD把所有文章的特征向量放在一起，为 其中M是文章数，N是词数。

奇异值分解可以把A分解为 ， 其中K1是主题数，K2是语义类数，X是每个文章和每个主题的相关性，Y是词和语义类的相关性，

信息指纹和相似哈希

信息指纹用伪随机数产生算法将一段信息压缩成一段数字。可以证明，只要算法足够好，就能保证两个不同信息的指纹相同的概率极小。将一个集合的所有元素的信息指纹相加就能用于集合相同的判定（加法的交换律）。而进行多次随机挑选比较 就是判定两个集合是否基本相同。

而相似哈希就是将每个元素的信息指纹按权重（可能是TF-IDF）逐位相加，可以用于度量相关性（差越小相关性越大）（但是应该只能度量 比较相似 和 不相似 吧）。伪代码大致如下：

1
ans[j] += (((hash[i]>>j)&1)?1:-1)*w[i];

后面没时间了，简单写写

RSA算法

其中为选定的很大的素数取满足为的逆元，即以为公钥，为私钥加密：解密：

P，Q很大，所以虽然N是公开的，但是不能知道M。最后两行用到了费马小定理。

最大熵原理

在所有可能的概率模型中，熵最大的模型概率最好（不确定性）。（猜测骰子概率）

也可以用于综合多种数据（比如拼音输入法的通用模型和个性化模型）。

公式为（可能？）

参数 可以用通用迭代算法GIS训练。

布隆过滤器

用于判断一个元素是否存在于一个集合里

把一个8字节的url变成8个信息指纹（），存到一个大小为16*N的哈希表（桶）里

为啥是16*N呢？因为作者说的哈希表的存储效率只有50%。

保证不会漏，但是可能会多（概率很小）。

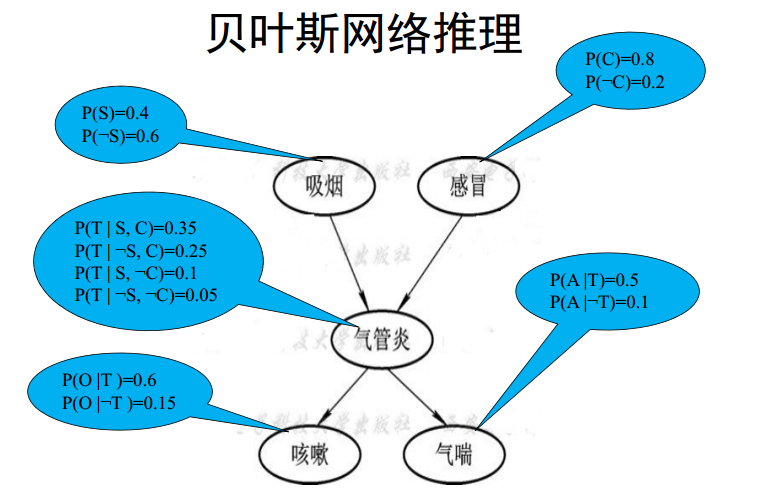
贝叶斯网络

跟马尔可夫链挺像的，基于”一个状态只由指向它的状态所直接决定。

但不完全一样，边权那里更复杂。

实例

杂记

简单有效的东西

作者认为，有的时候简单的算法会比精确而复杂的方法更有效，因为这容易读懂，易维护。而大而全的方法不仅容易因长时间不能完成而不了了之，而且可能会陷入像大圆套小圆那样冗杂的方法中。辛格甚至要求对于改进方法都要有清楚的理由，对于参数和公式都要有合理的物理解释，不然难以改动，容易变成“凑合”的算法。

个性化语言模型

一个用户的输入内容有限，可以把输入内容和用语习惯类似的用户合并在一起。（我认为这里信息量增加的原因可能是人类的群居性或者叫做标签化（类似于“人以类聚”）。

没看懂的地方

不代表其他都看懂了，只是这些完全没看懂

  • 基于变换规则的机器学习方法

  • 条件随机场

没时间总结的地方

  • 码分多址
    • 无线电通信相关
    • 基于扩频传输
    • 多频带，多信息同时传输，用对应地址码解调出相应信号
  • 期望最大化算法
    • 可以应用于文本的自收敛分类
      1. 先随机选K个点作为初始中心
      2. 将每个点归到最近的中心
      3. 重新计算每一类的中心
      4. 一直重复23步，直到同一类中各个点到中心的平均距离d最小，不同类中心之间的平均距离D最大
  • 逻辑回归模型
    • 用于把一个数值映射到一个0-1概率上？
  • 人工神经网络
    • 输入层，输出层，隐藏层
    • 通过边权计算点权 G=f(g(w1,w2,...)) 其中g是线性变换，f是一对一的函数（通常是e^x)
    • 通过设计成本函数可以进行无监督训练
  • 椭圆曲线加密原理
≡