无人机笔记

文章发布时间:

最后更新时间:

函数

  • void rotation_yaw(float yaw_angle, float input[2], float output[2]);

    坐标系旋转函数- 机体系到enu系

    input是机体系,output是惯性系，yaw_angle是当前偏航角

  • void collision_avoidance(float target_x, float target_y)

    避障的同时到(target_x, target_y)

雷达

  • Laser.ranges[i] ：range_min到range_max的距离
  • distance_c，angle_c：最小距离和所对角

位置

  • pos_drone.pose.position.x或y

  • Euler_fcu：欧拉角（Euler angles）是一种用于描述物体在三维空间中旋转的方法。它由三个角 度组成，通常表示为 α、β 和 γ，也被称为滚转（roll）、俯仰（pitch）和偏航（yaw）。

    • 滚转角（Roll）表示物体绕其自身坐标系的 X 轴旋转的角度。
    • 俯仰角（Pitch）表示物体绕其自身坐标系的 Y 轴旋转的角度。
      • 偏航角（Yaw）表示物体绕其自身坐标系的 Z 轴旋转的角度。

命令（出口）

command_pub ### 悬停

1
2
3
4
5
6
7
for (int i = 0; i < 5; i++)
{
    Command_now.command = Hold;
    Command_now.sub_mode = 0x00;
    command_pub.publish(Command_now);
    rate.sleep();
}

移动

1
2
3
4
5
6
7
8
9
Command_now.command = Move_ENU; // 机体系下移动
Command_now.comid = comid;
comid++;
Command_now.sub_mode = 2; // xy 速度控制模式 z 位置控制模式
Command_now.vel_sp[0] = vel_sp_ENU[0]; // collision_avoidance()里设置的
Command_now.vel_sp[1] = vel_sp_ENU[1]; // ENU frame
Command_now.pos_sp[2] = fly_height;
Command_now.yaw_sp = 0;
command_pub.publish(Command_now);

视觉

  • 来使 darknet_boxes 存储各个图片的信息，用 detect_num 存储相机共检测到的图片数目

  • darknet_boxes.bounding_boxes[i]的类型是 darknet_ros_msgs 中的 BoundingBox 消息类型中，通常包含以下字段：

  • header：消息头，包含了时间戳和坐标系信息。

  • Class：检测到的目标的类别或标签。

  • xmin：边界框的左上角 x 坐标。

  • ymin：边界框的左上角 y 坐标。

  • xmax：边界框的右下角 x 坐标。

  • ymax：边界框的右下角 y 坐标。

  • probability：目标的检测置信度或概率。

1
2
3
4
5
6
7
darknet_ros_msgs::BoundingBox fire_box = darknet_boxes.bounding_boxes[i];
if (fire_box.Class != "person")
    continue;
float dx = Laser.ranges[0] * cos(Euler_fcu[2]);
float dy = -dx * ((fire_box.xmin + fire_box.xmax) / 2 - cx) / fx;
float fire_center_x = pos_drone.pose.position.x + dx;
float fire_center_y = pos_drone.pose.position.y + dy;

​

路径规划算法

参考 ### 构型空间 机器人的所有状态（构型）的集合 比如 \(\{(无人机的x坐标,y坐标,所朝方向\theta)\}\)

PRM

  1. 在图中随机采样一定数量（如50个）的无碰撞点。
  2. 对每一个点，取其领域（相邻区域）内（例如直线距离在200以内）的所有点进行连线，对连线进行碰撞检测（如果连线与碰撞点有相交就删除连线），将结果存放在邻接矩阵中。 ### RRT 在每次选择生长方向时，有一定的概率会向着目标点延伸，也有一定的概率会随机在地图内选择一个方向延伸一段距离 假设我们采样了空间中随机一个点，接下来从现有的RRT树中选择离采样点最近的一个点，并向采样点延伸一段距离。假如在这段延伸中没有发生碰撞（碰撞检测），而且新点与现有的所有点的距离大于某个判断阈值（防止生长到RRT已经探索过的位置），则将这个新点也加入RRT树。 假如本次延伸的新点与终点的距离小于这个阈值，我们就认为已经规划成功。

这里利用统计学中回归分析生成新节点，将RRT算法探索未知空间的能力进一步增强以避免因启发估价因子导致的局部极小。其思想是探索以前到过的空间是无用的，而且容易陷入局部极小。引进回归分析(regression analysis)是考察新节点与其他节点之间关系，利用回归函数约束，使得随机树不探索以前到过的空间，因此避免了局部极小。

滚动RRT

滚动窗口状态空间进行K次采样后，遍历随机树，根据启发估价思想寻找滚动窗口子目标 \(X_{sub}\)。 \(X_{sub}\) 是当前滚动窗口中的子树中估价函数最小的点。确定子目标后，机器人前进到子目标点，进行下一轮的滚动RRT规划。如此反复，直到到达目标点 G。

人工势场

但是复杂的势场环境可能在目标点之外产生局部极小点导致机器人无法到达目标。遇到局部极小点后结合其他的方法使机器人离开局部极小点。沿墙行走法使机器人在遇到局部极小点后参照类似BUG算法的环绕行为绕过产生局部极小点的障碍物继续前进。这种方法可靠性高，不依赖环境的先验信息和障碍物形状。

为了使机器人从局部极小点中逃离，在人工势场法的基础上引入应激行为，即增加绕行行为。当机器人遇到局部极小点时，忽略目标引力势的作用，沿着斥力势的等势面方向移动，直到机器人离开局部极小区域。

  1. 根据传感器信息计算当前位置的引力和斥力；
  2. 判断是否处于绕行行为，若是，执行3；若否，执行4；
  3. 判断是否离开局部极小区域，若是，机器人沿着合力方向运动，结束绕行行为；若否，机器人沿着斥力场等势线运动，继续绕行行为；
  4. 判断是否遇到局部极小点，若是，机器人沿着斥力场等势线运动，开始绕行行为；若否，机器人沿着合力方向运动；
  5. 判断是否到达目标，若是，退出算法；若否，继续1；

\(\left| f_{att}+\sum_{j=1}^{n}{f_{rep,j}} \right|<\varepsilon\) \(\left| x-x_A \right|<\alpha s_A\) 当条件1或者条件2出现时，就认为机器人遇到了局部极小点。条件1中 \(\varepsilon\) 是一个很小的正数，其含义是机器人受到的虚拟合力接近0。这是最直接局部极小点判断方法。条件2中 \(\alpha\) 为0,1之间某一正数， x_A 为机器人运动过程中某一状态， s_A 表示机器人从 x_A 到达当前位置 x 的总路程，条件2成立意味着机器人在运动很长路程后，位移很小。用来检测机器人在局部极小点附近发生的振动和圆周运动。

BUG算法

BUG算法是一种完全应激的机器人避障算法。其算法原理类似昆虫爬行的运动决策策略。在未遇到障碍物时，沿直线向目标运动；在遇到障碍物后，沿着障碍物边界绕行，并利用一定的判断准则离开障碍物继续直行。这种应激式的算法计算简便，不需要获知全局地图和障碍物形状，具备完备性。但是其生成的路径平滑性不够好，对机器人的各种微分约束适应性比较差。

图片

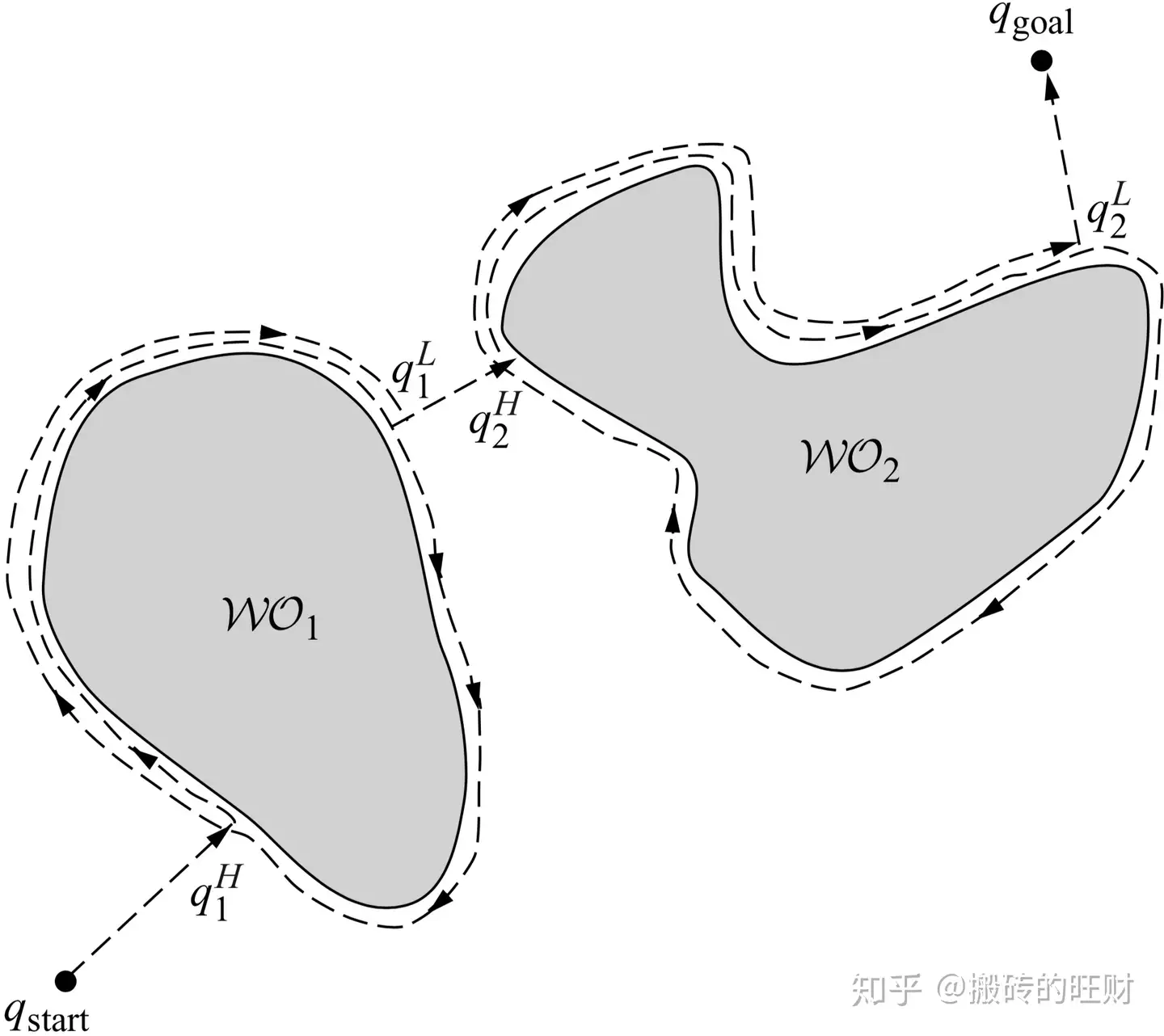
（沿着障碍物绕一圈）

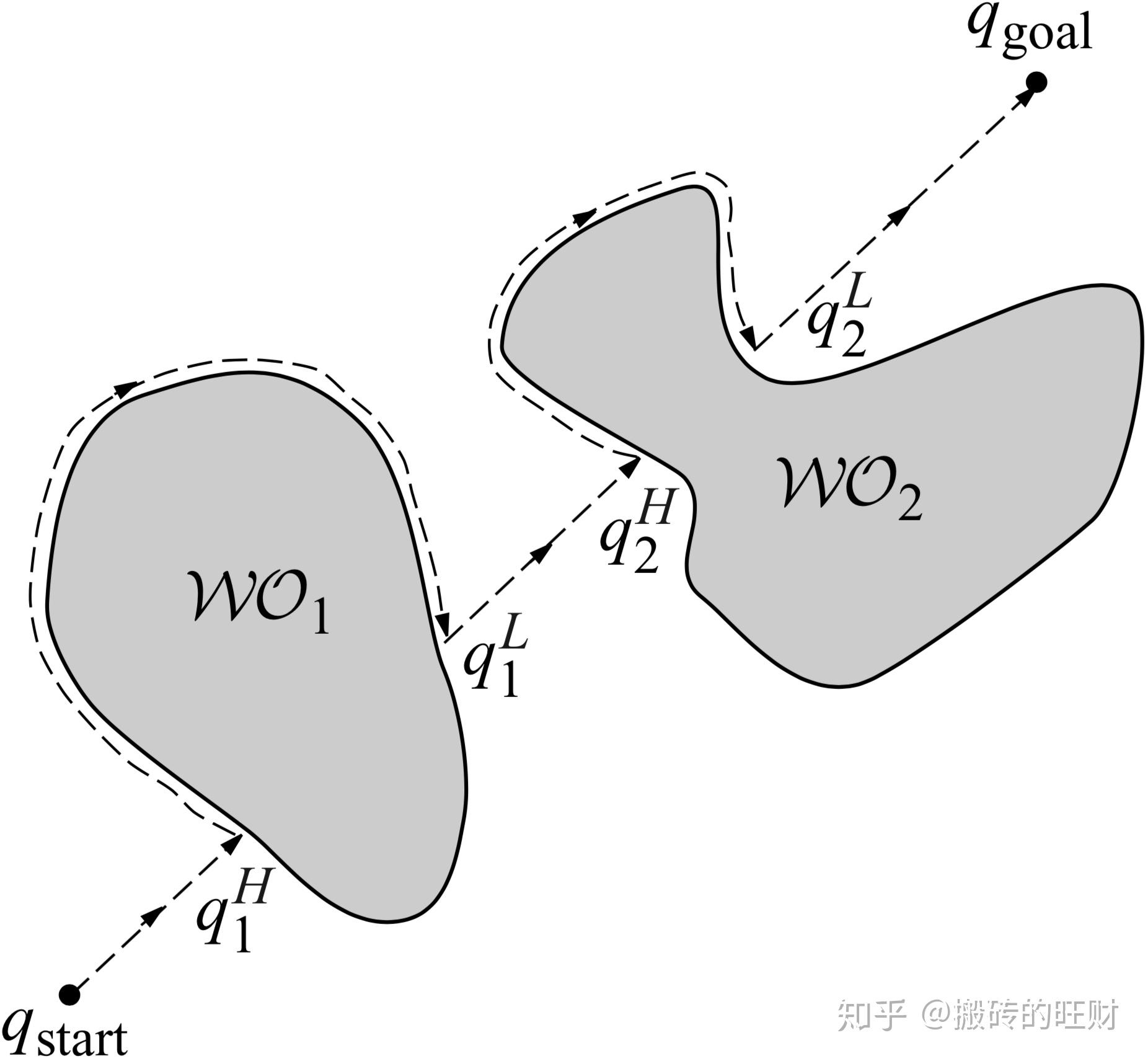bug2 bug2 直到碰到直线

TangentBUG算法

  • 雷达扫描 找到距离的间断点（角度）
  • 选择一个角度，用 从当前位置经过此角度上的交点到目标点的折线长度 判断走哪个角度
  • 探索距离不再减小时，就停止向目标运动行为，切换到环绕边界行为
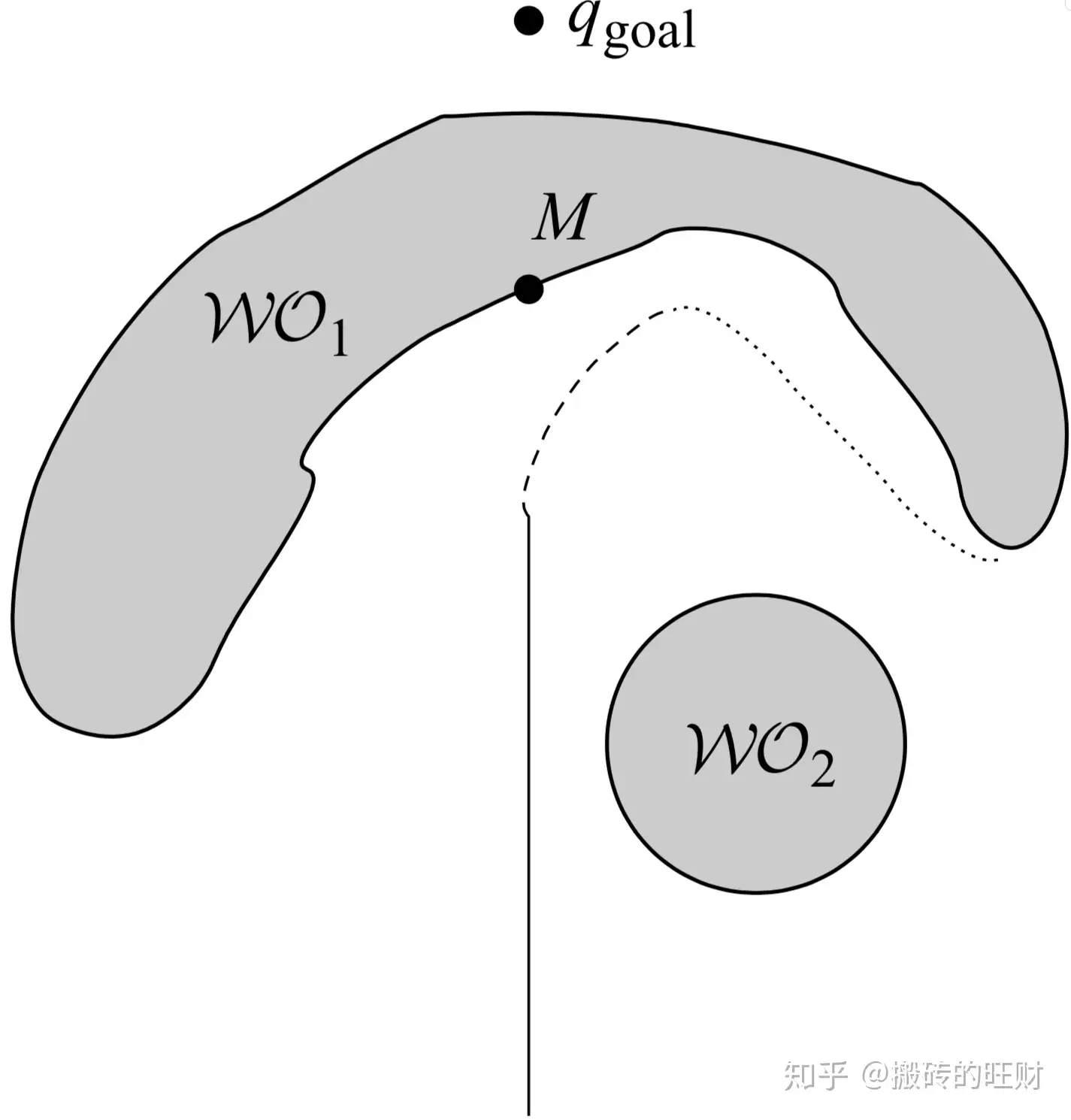
  • 如下图所示，当机器人探索到障碍物上的 M 点后，探索距离就不再减小，即 � 点是机器人探索距离在障碍物边界上的局部极小点。机器人开始沿着障碍物边界进行环绕，图中虚线路径就是机器人环绕障碍物时所走的路径。当机器人探测到与目标距离相比 � 点更近的点时，重新开始接近目标的运动。
    • bug2

卡尔曼滤波

  • 高斯分布：卡尔曼滤波假设两个变量（位置和速度，在这个例子中）都是随机的，并且服从高斯分布。每个变量都有一个均值 μ，表示随机分布的中心（最可能的状态），以及方差 \(\sigma^2\)，表示不确定性。
  • 协方差矩阵
    • ![[Pasted image 20240302153643.png]]
    • 矩阵中的每个元素 \(\Sigma_{i,j}\) 表示第 i 个和第 j 个状态变量之间的相关度
  • ![[Pasted image 20240228133157.png|200]]
  • ![[Pasted image 20240228134002.png|200]]
  • 控制变量和控制矩阵 ![[Pasted image 20240228134327.png|200]]
  • 外部干扰 ![[Pasted image 20240228134545.png|200]]
  • 传感器检测 ![[Pasted image 20240228162415.png|400]] ![[Pasted image 20240228162527.png|300]] 其中 \(H_k\) 把预测数据转化为相对应的传感器数据 ![[Pasted image 20240228163108.png]]
  • 总结与应用 用于建图时定位

杂记

  • NED系（North-East-Down）ENU：East-North-Up
≡