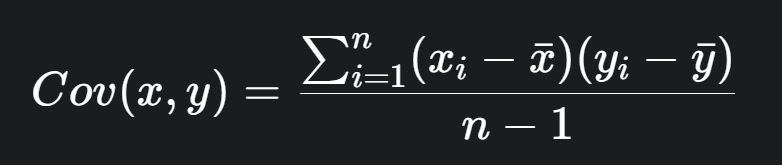Cov(x,y) 是第一个和第二个分量之间的协方差

好的，我们来计算协方差矩阵 Σ=(2.54.25​4.257.3​) 的特征值和对应的特征向量，并指出第一个主成分方向。

1. 计算特征值：

特征值 λ 是通过解以下特征方程得到的：

det(Σ−λI)=0

其中，I 是 2×2 的单位矩阵。

所以，我们得到两个特征值：

λ1​=29.8+9.76166​≈219.56166​≈9.78083 λ2​=29.8−9.76166​≈20.03834​≈0.01917

2. 计算对应的特征向量：

对于每个特征值 λ，我们需要解 (Σ−λI)v=0 来找到对应的特征向量 v=(v1​v2​​)。

对于特征值 λ1​≈9.78083：

这给我们两个线性方程：

\(−7.28083v1​+4.25v2​=0\) \(4.25v1​−2.48083v2​=0\)

从第二个方程，我们可以得到：

v1​≈0.5837v2​

如果我们令 v2​=1，那么 v1​≈0.5837。所以，对应于 λ1​ 的特征向量 v1​ 大致为：

v1​≈(0.58371​, 1)

主成分是与协方差矩阵的特征向量相对应的方向，特征值的大小表示了该方向上的数据方差。第一个主成分方向是与 最大 特征值相对应的特征向量。

1. 计算总方差：

总方差是所有特征值的总和。在主成分分析中，总方差代表了原始数据集中总的信息量（或者说总的散布程度）。

总方差 =λ1​+λ2​≈9.78083+0.01917=9.8

2. 计算每个主成分的方差贡献率：

每个主成分的方差贡献率是该主成分的特征值占总方差的比例。它表示了该主成分所解释的原始数据变异性的百分比。

第一个主成分的方差贡献率：

​λ1/(λ1​+λ2)​​×100%≈9.89.78083​×100%≈0.99804×100%≈99.804%

第二个主成分的方差贡献率：

λ2/(λ1​+λ2)​​​×100%≈9.80.01917​×100%≈0.001956×100%≈0.196%

3. 解释方差贡献率的意义：

• 第一个主成分的方差贡献率约为 99.804%。 这意味着第一个主成分单独就解释了原始数据中大约 99.804% 的变异性。换句话说，原始数据的大部分信息都能够被这个主成分所捕获。如果我们只保留第一个主成分，我们仍然能够保留原始数据中绝大部分的散布和模式。

• 第二个主成分的方差贡献率约为 0.196%。 这表明第二个主成分只解释了原始数据中非常小的一部分变异性（约 0.196%）。这意味着在第一个主成分已经捕获了几乎所有重要信息后，第二个主成分所包含的额外信息量非常有限。